14  Inference

14.1 Classic Inference

The word “inference” in general refers to drawing conclusions from logical reasoning. In statistics, it refers to drawing conclusions in the presence of uncertainty. Why is there uncertainty in the first place? The main reason is sampling uncertainty. Recall the following definitions.

  • Population. The universe of units that are of interest. There is a parameter of interest in the population, such as the true probability that a flipped coin lands on heads.
  • Sample. A subset of the population. We use the sample to estimate the parameter of interest using a statistic, such as the proportion of times that a flipped coin landed on heads after many trials.

Sampling uncertainty arises whenever there is a sample because there is no guarantee that a sample is representative of the population. Even if all of the observed characteristics are identical, there could be unobserved characteristics that diverge between the sample and the population. Despite this, we rely on data from samples because in most cases, it is very difficult or impossible to collect data on the entire population of interest. As long as we use statistics to quantify the uncertainty, samples do the trick.

14.1.1 Example: Fair/Unfair Coin

Suppose you procure a coin that you believe is unfair. You flip it 10,000 times and get heads 52% of the time. We will use this sample to make some inference about the parameter of interest.

  1. Establish the research question. Is the coin fair? That is, you get heads on average 50% of the time?
  2. Define the parameter of interest. The true probability, \(\pi\), that the suspicious coin is heads.
  3. Calculate the statistic. We observe heads 52% of the time in the sample. That means that the statistic is the estimated probability that the coin is heads, \(\hat{\pi} = 0.52\).
  4. Set up the null and alternative hypotheses. A hypothesis should be in reference to the population parameter. You should put the statement you are challenging in the null hypothesis. The aim is not to “accept” the alternative hypothesis. Rather, we see if we can reject the null hypothesis at some level of confidence.

\[\begin{align*} H_0: \pi &= 0.5 \\ H_1: \pi &\neq 0.5 \end{align*}\]

  1. Compute the test statistic for the hypothesis test. This involves calculating a \(t\)- or \(Z\)-statistic, which can then be used to calculate a \(p\)-value or a confidence interval. Technically, the \(Z\)-statistic is appropriate when the population variance is known and the \(t\)-statistic is appropriate when the population variance is unknown. Usually, they yield the same results because the Student’s \(t\) distribution converges to the Normal distribution (required for the \(Z\)-test). I write both below for clarity. You can see that they produce very similar results. Only for small sample sizes will the choice of test make a difference.

Recall that for a Bernoulli random variable, which describes a coin flip, the mean is \(\pi\) and the standard deviation is \(\pi(1-\pi)\). Recall that the standard error is the standard deviation divided by the square root of the sample size, \(n\).

\(Z\)-statistic (Normal distribuion):

\[\begin{equation*} Z = \frac{\hat{\pi} - \pi}{\sqrt{\frac{\pi(1-\pi)}{n}}} = \frac{0.52 - 0.5}{\sqrt{\frac{0.25}{10000}}} \end{equation*}\]

(0.52 - 0.5) / sqrt(0.25 / 10000)
[1] 4

\(t\)-statistic (Student’s \(t\) distribution with \(n-1\) degrees of freedom):

\[\begin{equation*} t = \frac{\hat{\pi} - \pi}{\sqrt{\frac{\hat{\pi}(1-\hat{\pi})}{n}}} = \frac{0.52 - 0.5}{\sqrt{\frac{0.2496}{10000}}} \end{equation*}\]

(0.52 - 0.5) / sqrt(0.2496 / 10000)
[1] 4.003204
  1. Compute \(p\)-value or confidence to report the conclusion from the hypothesis test. For a two-sided test (remember that the distributions for both tests are symmetric), consider \(Z\) to be a random variable distributed according to a standard Normal distribution. The \(p\)-value is

\[\begin{align*} \Pr\left(Z > \frac{\hat{\pi} - \pi}{\sqrt{\frac{\pi(1-\pi)}{n}}} \quad \bigcup \quad Z < \frac{\hat{\pi} - \pi}{\sqrt{\frac{\pi(1-\pi)}{n}}}\right) = 2 \Pr\left(Z > \frac{\vert\hat{\pi} - \pi\vert}{\sqrt{\frac{\pi(1-\pi)}{n}}}\right). \end{align*}\]

You may recall using statistical tables in the back of your textbook or online to compute \(p\)-values. You can use R for it too! The below functions compute the lower tail probability. So for some input quantile \(x\), pnorm(x) gives \(\Pr(Z \leq x)\). You can use the symmetry to get the \(p\)-value or change the argument lower.tail=FALSE. I show both ways below.

# Normal distribution
2 * pnorm(4, lower.tail = FALSE)
[1] 6.334248e-05
2 * (1 - pnorm(4))
[1] 6.334248e-05
# Student's t distribution with n-1 degrees of freedom
2 * pt(4.003, df = 99, lower.tail = FALSE)
[1] 0.0001209255
2 * (1 - pt(4.003, df = 99))
[1] 0.0001209255

It is common to use certain cut-offs for \(p\)-values, such as 0.1, 0.05, 0.01, or 0.001. Given how small the \(p\)-value is here, it is common to see them reported as \(p < 0.001\). We can reject the null hypothesis at the 99.9% level.

Analogously, we can construct a confidence interval around the estimated statistic. For a two-sided \(Z\)-test:

\[\begin{align*} CI_{\alpha} = \left[\hat{\pi} - z^*_{\alpha/2} \sqrt{\frac{\pi(1-\pi)}{n}}, \hat{\pi} + z^*_{\alpha/2} \sqrt{\frac{\pi(1-\pi)}{n}} \right] \end{align*}\]

  • \(\alpha\) is the threshold to reject the null hypothesis. For example, if \(\alpha = 0.05\), then the \(p\)-value has to be less than 0.05 to reject the null hypothesis.
  • \(z^*_{\alpha/2}\) the “critical value” in the standard normal distribution such that \(\Pr(Z > z^*) = \alpha/2\). In the normal distribution for \(\alpha = 0.05\), \(z^* = 1.96\).

The confidence interval is analogous for the \(t\)-test, but use the critical value from the Student’s \(t\)-distribution. The confidence interval for a one-sided test will sue the critical value \(z^*_{\alpha}\). The lower bound will be \(-\infty\) if the alternative hypothesis is \(\leq\) or the upper bound will be \(\infty\) if the alternative hypothesis is \(\geq\).

Let us use R to construct the 95% confidence interval. Notice we use qnorm() and `qt() to get the quantile of the distribution given a probability. For both cases, it is approximately \([0.495, 0.545]\).

# Normal distribution
0.52 - qnorm(0.05/2, lower.tail = FALSE) * sqrt(0.25 / 10000)
[1] 0.5102002
0.52 + qnorm(0.05/2, lower.tail = FALSE) * sqrt(0.25 / 10000)
[1] 0.5297998
# Student's t distribution
0.52 - qt(0.05/2, df = 99, lower.tail = FALSE) * sqrt(0.2496 / 10000)
[1] 0.5100869
0.52 + qt(0.05/2, df = 99, lower.tail = FALSE) * sqrt(0.2496 / 10000)
[1] 0.5299131

If the confidence interval overlaps the true parameter, then we cannot reject the null hypothesis. Because 0.5 is not in the confidence interval, we can reject the null hypothesis with 95% confidence.

  1. Conclude. Because we reject the null hypothesis, we reject that the coin is fair at the 99.9% confidence level using the \(p\)-value.

14.2 Bootstrapping

In many cases, the \(Z\)-test or \(t\)-test are adequate for hypothesis testing. However, they rely on assumptions about the distribution of the estimator. If we have the sample mean, like we do for the coin example above, that is completely fine due to the Central Limit Theorem. What if we are interested in another statistic, like the median? Bootstrapping provides a non-parametric approach for these situations.

14.2.1 Example: Bootsrapping the Fair/Unfair Coin

Suppose the same set-up as above. Let us do the same test with bootstrapping. However, we need the data in order to do the bootstrapping, so let me simulate it here. In reality, we do not know \(\pi\), the true probability of getting heads. To simulate data, we need to specify this probability. Suppose it is 0.53. We get a sample mean of 0.523.

library(dplyr)

Attaching package: 'dplyr'
The following objects are masked from 'package:stats':

    filter, lag
The following objects are masked from 'package:base':

    intersect, setdiff, setequal, union
set.seed(470500) # Remember to set the seed so that the results are reproducible

# Define the data

pi_true <- 0.53

# 0 is tails, 1 is heads
flips <- rbinom(10000, size = 1, prob = pi_true)

# pi hat is the sample average
pi_hat <- mean(flips)
pi_hat
[1] 0.523
# I will make flips a tibble to be clear about the bootstrap steps below
flips_tib <- tibble(flip_id = 1:10000,
                    outcome = flips)
  1. (Same as above) Establish the research question. Is the coin fair? That is, you get heads on average 50% of the time?
  2. (Same as above) Define the parameter of interest. The true probability, \(\pi\), that the suspicious coin is heads.
  3. (Same as above) Calculate the statistic. We observe heads 52% of the time in the sample. That means that the statistic is the estimated probability that the coin is heads, \(\hat{\pi} = 0.523\).
  4. (Same as above) Set up the null and alternative hypotheses. A hypothesis should be in reference to the population parameter. You should put the statement you are challenging in the null hypothesis. The aim is not to “accept” the alternative hypothesis. Rather, we see if we can reject the null hypothesis at some level of confidence.

\[\begin{align*} H_0: \pi &= 0.5 \\ H_1: \pi &\neq 0.5 \end{align*}\]

  1. Bootstrap. The idea behind bootsrap is that we take the distribution in the data from the sample as given and do not impose any assumptions. This means that if we resample the sample we are essentially taking a new draw from the underlying distribution. Each bootstrap is one resample. We resample with replacement. That means we can get repeated observations. For example, the bootstrap could contain four instances of the first coin flip. First of all, if we take the sample distribution seriously, then each instance is random. That means that it is also random to get more than one of the isntance. Second, if we were resample without replacement, then we would get the exact same sample each time. Because we are interested in the average of the population as the parameter of interest, we take the sample mean of the bootstrap.
set.seed(407500)

# Resample the IDs
b1_ids <- sample(flips_tib$flip_id, size = nrow(flips_tib), replace = TRUE)

# Notice how we could theoretically get more than one instance
head(table(b1_ids))
b1_ids
1 2 3 4 5 7 
1 1 2 2 2 1 
# We don't want the IDs, we just want the outcomes of the flips
b1 <- flips_tib$outcome[b1_ids]

# Calculate the sample mean for this bootstrap
b1_mean <- mean(b1)
b1_mean
[1] 0.5167

That was one bootstrap. We want many bootstrap resamples. Let us select \(B = 1,024\). It is conventional to choose exponents of 2 for the number of bootstraps. This has efficiency reasons that are outside the scope of this class.

library(magrittr) # optional, but I want to use pipes

set.seed(470500)
B <- 1024

bs <- vector()

for (b in 1:B) {
  
  bs[b] <- sample(flips_tib$outcome, size = nrow(flips_tib), replace = TRUE) %>%
              mean()
  
}

# Let us plot the density of the sample means from all the bootstraps

plot(density(bs), main = "Density of Bootstrap Means")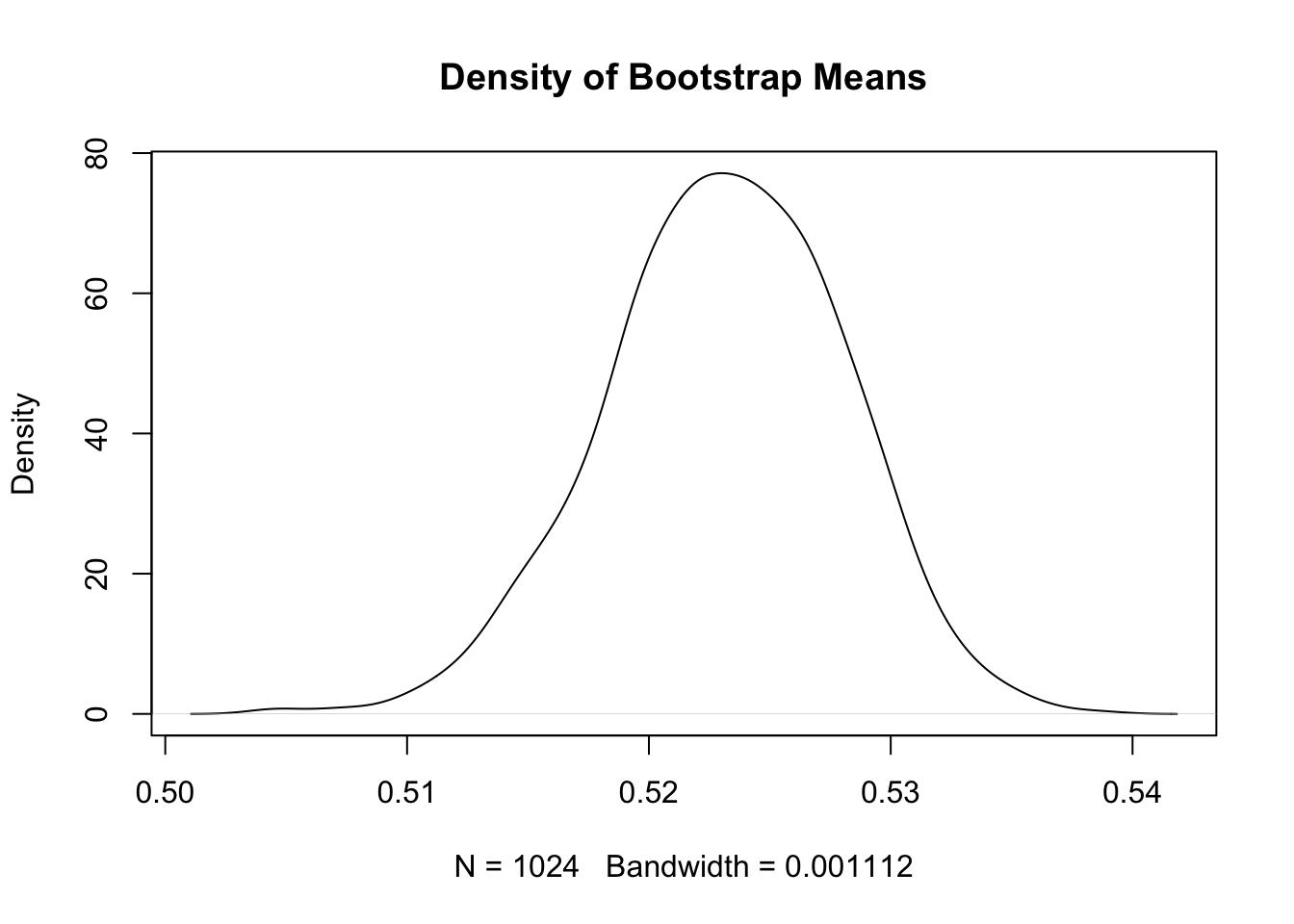

Density plot of bootstrap sample means, approximately normal with a peak around 0.522.

  1. Compute \(p\)-value or confidence to report the conclusion from the hypothesis test. Instead of using the Normal distribution or Student’s \(t\) distribution, we will use the bootstrap distribution. A similar logic holds. We want to know if what we observe in the sample is unlikely if the null hypothesis were to be true. The \(\alpha\)-level confidence interval is simply the \(\alpha/2\) and the \(1-\alpha/2\) quantiles.
# 95% confidence interval
quantile(bs, c(0.025, 0.975))
     2.5%     97.5% 
0.5130725 0.5323000

The bootstrapped \(p\)-value is outside the scope of this class.

  1. Conclude. Because 0.5 is outside the 95% confidence interval, we reject the null hypothesis, we reject that the coin is fair at the 95% confidence level.

14.3 Activity: Bootstrapping

  1. Calculate the median of the distribution of amount won.

  2. Suppose we want to test if the median is equal to 1,100. What are the null and alternative hypotheses?

  3. Write a loop to draw 1,024 bootstrap resamples. Here is an outline of the code. You fill in the commands.

# Set a seed

# Set the number of bootstraps

# Define an empty vector to store the output

# Start the loop

    # Inside the loop:
        
    # Resample df$AmountWon with replacement

    # Take the mean of the resample

    # Store the mean to the vector
  1. Calculate the 95% confidence interval. What do you conclude?

14.4 References

The data on lottery winners come from the Texas Data Portal. See Casella and Berger (2002) for a formal discussion of inference.

Casella, George, and Roger L. Berger. 2002. Statistical Inference. Second edition. Duxbury Advanced Series. Andover Melbourne Mexico City Stamford, CT Toronto Hong Kong New Delhi Seoul Singapore Tokyo: CENGAGE Learning. https://www.cengage.com/c/statistical-inference-2e-casella-berger/9780534243128/.